Retour

    Soit f et g deux fonctions définies sur un ensemble D de courbes représentatives C_f et C_g.
   

Courbe

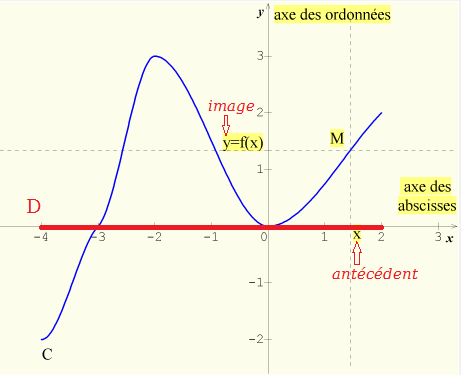
    Un point M(x;y) appartient à la courbe C_f si et seulement si x appartient à D et y = f(x).
    L'abscisse x est un antécédent de y par f.
    L'ordonnée y est l'image de x par f.
    L'ensemble de définition D est l'ensemble des abscisses des points de la courbe C_f ,
    c'est-à-dire l'ensemble des valeurs de x qui ont une image par f.

   

Sens de variation

    f est strictement croissante sur un intervalle I si pour tous réels x₁ < x₂ dans I , on a f(x₁) < f(x₂).
    f est strictement décroissante sur un intervalle I si pour tous réels x₁ < x₂ dans I , on a f(x₁) > f(x₂).
   

Exemple :

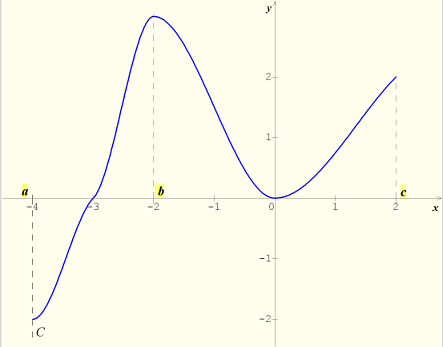
    Sur le graphique ci-dessous , la fonction f est strictement croissante sur [a;b] et sur [0;c] ,
    elle est strictement décroissante sur [b;0].

    Nous pouvons résumer ces informations dans un tableau de variations :

   

Signe

    f est strictement positive sur un ensemble E si pour tout réel x de E , on a f(x) > 0.
    Graphiquement , sur E , la courbe C_f est au-dessus de l'axe des abscisses.

    f est strictement négative sur un ensemble E si pour tout réel x de E , on a f(x) < 0.
    Graphiquement , sur E , la courbe C_f est au-dessous de l'axe des abscisses.
   

Exemple :

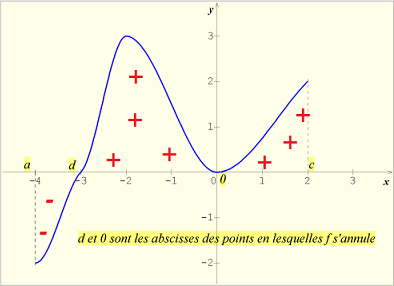
    Sur le graphique ci-dessous , la fonction f est strictement positive sur ]d;0[ et sur ]0;c] ,
    elle est strictement négative sur [a;d[ , elle s'annule en d et 0.

    Nous pouvons résumer ces informations dans un tableau de signes :

   

Résoudre l'équation f(x) = k , où k est un réel fixé :

    C'est trouver tous les réels x dont l'image par f est égale à k.
    Graphiquement , c'est trouver les abscisses des points de C_f situés sur la droite d'équation y = k.
   

Résoudre l'inéquation f(x) < k , où k est un réel fixé :

    C'est trouver tous les réels x dont l'image par f est strictement inférieure à k.
    Graphiquement , c'est trouver les abscisses des points de C_f situés au-dessous de la droite d'équation y = k.    

Exemple :

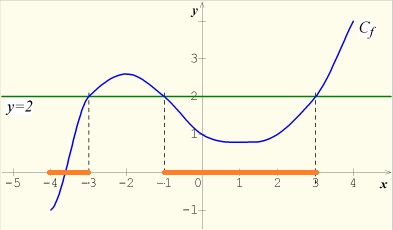
    Une fonction f est définie sur l'intervalle [- 4;4] par la courbe ci-dessous.
    L'équation f(x) = 2 admet pour ensemble solution S = { - 3 ; - 1 ; 3 }.
    L'inéquation f(x) < 2 admet pour ensemble solution S = [ - 4 ; -3 [ U ] - 1 ; 3 [.

   

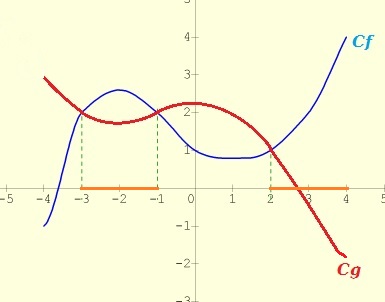
Résoudre l'équation f(x) = g(x) ,

    C'est trouver tous les réels x dont l'image par f est égale à l'image par g.
    Graphiquement , c'est trouver les abscisses des points d'intersection de C_f et C_g.
   

Résoudre l'inéquation f(x) > g(x) ,

    C'est trouver tous les réels x dont l'image par f est strictement supérieure à l'image par g.
    Graphiquement , c'est trouver les abscisses des points de C_f situés au-dessus de C_g.    

Exemple :

    Deux fonctions f et g sont définies sur l'intervalle [- 4;4] par leurs courbes ci-dessous.
    L'équation f(x) = g(x) admet pour ensemble solution S = { - 3 ; - 1 ; 2 }.
    L'inéquation f(x) > g(x) admet pour ensemble solution S = ] - 3 ; -1 [ U ] 2 ; 4 ].

    Attention ! Une résolution graphique est en général une résolution approchée.